電磁波の研究(確定版)
はじめに
電磁波の伝播特性を研究します。光の屈折・反射・分光・ドップラー現象等の電磁波の性質整理し、運動する発生源から発する
電磁波の速度の理論を説き、天体と地上の物理現象を考察します。研究の要旨は「電磁波の速度は電磁的伝搬速度と
発生源の運動速度を合わせたものである。」です。
本論を世に問い、実証されることを希望します。
項目
1.電磁波の理論
1)電磁波の性質
2)電磁波と光
3)電磁波の生成
4)伝播速度
5)運動する発生源からの電磁波
6)横移動する電磁波
7)放射電磁波の軌跡
8)電磁波のドップラー現象
9)電磁波の減衰と周波数・波長の変化
2.天体の運行
1)光差
2)光行差
3)連星の公転
4)銀河の回転曲線
5)環状銀河
6)天体の光の減衰と周波数・波長の変化
3.地上の観測
1)地上における電磁波速度の計測
2)マイケルソンモーレーの実験
3)大砲の照準
4)放送波
5)GPSによる位置計測
6)ファイバーリングジャイロ
7)日本標準時(JJY)
4.検証
1)絶対静止系の検出
2)天体の光速度の計測
5.おわりに
1.電磁波の理論
天体・地球上における電磁波の諸現象を拠り所に新しい理論を提案します。
1)電磁波の性質
以下に示す電磁波の性質は実験的に観測される事象です。
(1)磁界と電界が振動して空間を移動する電気エネルギーである。
(2)質量は無いが運動量を持つ。
(3)電磁波の周波数の違いにより電波または光と呼ばれる。
(4)真空及び空気、液体、透明結晶等の物質を透過する。
(5)屈折、反射、拡散、回折、干渉の現象がある。
(6)伝播速度は環境の誘電率と透磁率によって定まり、真空中では30万km/秒で一定である。
(7)発生源または観測装置が運動するとき、ドップラー現象が起きる。
2)電磁波と光
一般に言われる電波は目に見えませんが、光は電磁波の一種であり人はその振動数の違いから感じることが出来ます。
(1)光の屈折
光は誘電率の異なる物質の界面で屈折し、混合光は屈折率が異なるため分光します。
図1-1 光の屈折と反射 で、屈折率nと電磁波速度は透磁率μと誘電率εで規定されます。
屈折率の変化を測定することによりドップラー現象を検知することが出来ます。
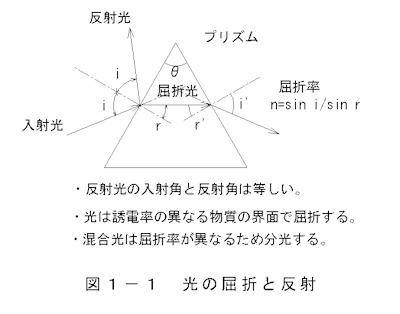 屈折率nは次式で表されます。
屈折率nは次式で表されます。
n=sin(i)/sin(r)
(1-1)
n=(με)0.5
(1-2)
電磁波の速度は次式で表されます。
c=co/(με)0.5
(1-3)
co;電磁波速度の固有値
真空ではμ=1,ε=1 となります。
(2)光の反射
鏡で反射される光(電磁波)の特性
・電磁波は完全弾性体とみなされ、入射角と反射角は等しく、発生源と鏡の運動は影響しない。
・反射する電磁波の速度は入射光の速度に鏡の速度が加算される。
図1-2 光の反射 で発生源から出る光が鏡Mで反射されるとき、鏡の運動速度の如何にかかわらず入射角と反射角は等しく
反射光の速度は入射速度に鏡の運動速度vが加わったものになる。また、反射角は入射光と鏡の角度により変化する。
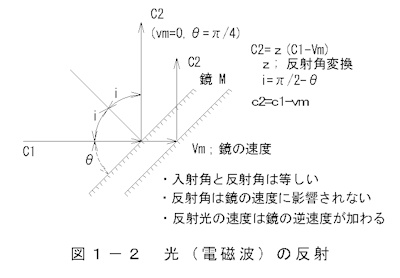 C2=z(C1-Vm) (1-4)
C2=z(C1-Vm) (1-4)
c2=c1+vm (1-5)
z ; 反射角の変換, θを光軸と鏡がなす角度とすると
i=π/2-θ (1-6)
c1; 入射光速度
C2; 反射光速度
Vm; 鏡の移動速度
水平の入射光は45°傾いている鏡では反射光が90°横向きになる。
図1-3 反射光の速度 で鏡に反射した光の速度はC2であるがその伝搬波形の様子を示している。

入射光と反射光の波形
x=A sin((2πy/λ1)t) (1-7)
x=A sin((2πy/λ2)t) (1-8)
となる。
電磁波の伝搬速度C1,C2は
C1=C+Vs (1-9)
C2=-(C1-Vm) (1-10)
C2=-C-Vs+Vm(1-11)
しかるに振動数νは一定とすると周期は
τ1=λ1/c1 (1-12)
τ2=λ2/c2 (1-13)
となる。
3)電磁波の生成
電磁波は電気的な発振器で生成され、光は電子が原子に直接作用するか又は原子が加熱されることにより原子内の電子が
励起することで生じます。電気エネルギーが振動する磁界と電界に変化したものが電磁波です。物質が質量のない電磁波に変化する
ということは電気エネルギーが振動エネルギーに変換されていると考えます。エネルギー E=hxν(h:プランクの定数、ν:振動数)
で表されます。図1-4 電磁波の生成 で、Z軸方向に進む電子(交番電流)がX-Y平面に磁界を作ります。
電磁波は電流の周りに発生した環状に放射された磁界となって電流軸を原点に一定の速度で伝搬します。また、伝搬する電磁波は
発生源の運動速度Vの方向に移動します。電磁波の合成速度はCvとなります。
注)速度は2点間を進む指標です。すなわち距離を所要時間で割ったものでそれらの位置(座標)に拠りません。
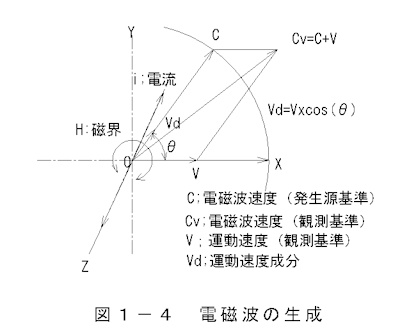 電磁波の速度
電磁波の速度
・地球基準(地球上で観測)
Cv=C+V (1-14)
・宇宙基準(他の天体で観測)
Cv=C+V+Ve (1-15)
・運動速度成分
Vd=V cos(θ) (1-16)
Cv ;電磁波の観測速度
C ;電磁波速度(発生源基準)
V ;発生源の速度(観測点基準)
Ve ;地球と他の天体との相対速度
Vd ;運動速度成分
θ ;偏角(電磁波方向と運動方向がなす角度)
4)発生源の移動方向と横に進む電磁波
発生源が横移動する電磁波の伝播を 図1-5 電磁波の横移動 に示します。前項から推察されますが、
電磁波は発光源の運動と共に平行移動すると考えます。
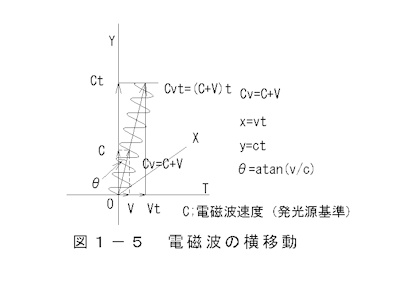 電磁波の波形は次式で表わされます。
電磁波の波形は次式で表わされます。
静止状態
x=A sin((2π y/λ)) (1-17)
右に移動するとき
x=A sin((2π y/λ))+v t (1-18)
5)電磁波の軌跡
運動する点光源からの電磁波の伝搬状態を 図1-6 電磁波の軌跡 に示します。
発生源は電磁波速度の38%で右(X軸)に進むものとします。電磁波の進む方向と運動のなす偏角θが0°から
2π(360°)までπ/6(30°)毎について作図したものを放射角θがπ/3(60°)で説明しています。
天体から観測する電磁波(見かけ速度)の軌跡は地上で観測した形状を運動速度Vで並行移動した形となります。
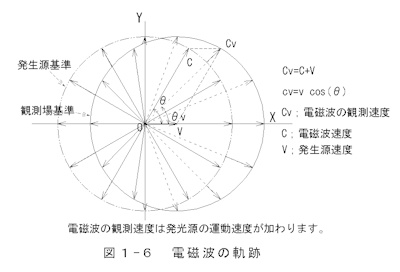
電磁波の伝搬は
Cv=C+V (1-19)
cv=(c2+v2+2c v cos(θ)) 0.5
(1-20)
θv=atan(c sin(θ)/(c cos(θ)+v)) (1-21)
で表されます。
見かけ速度は偏角θ=0°のとき最大となり、
cv=c+v (1-22)
θが180°のとき最小で
cv=c-v (1-23)
となります。
6)電磁波のドップラー現象
ドップラー現象は発生源または観測者が運動することで波長λが変化して観測される現象です。波長測定器(分光器)により
元来の波長と比較することで相対速度を知ることが出来ます。発生源が運動する場合と観測者が運動する場合の波長の変化は等価です。
図1ー7 電磁波のドップラー現象 で発生源と観測点の運動と電磁波速度の関係を図示します。
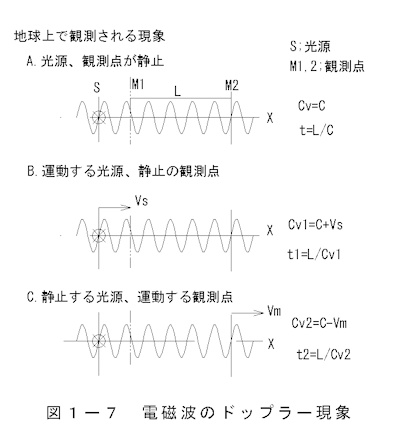
見かけの波長λは次式に表されます。
λ=λo c/(c+v)(1-24)
v=vs-vm (1-25)
λ、λo ;波長、元来の波長
c ;光速
v ;相対運動速度
vs,vm 発生源、観測点の速度
波形の形状は次式で表されます。
y=A sin((x+(vs-vm)t)/λ/2π)(1-26)
y ;電磁波の高さ
A ;波高値
x ;横位置
(1)発生源の運動と波長の変化
図1-7 で 電磁波の速度が変化すると波長が変化したように観測されます。
A. 発生源と観測装置が静止(相対速度が零)
波長に変化は見られません
y=A sin(x/λ/2π) (1-27)
B. 発光源が運動する場合
y=A sin((x+vs t)/λ/2π)(1-28)
電磁波速度が変化して波長が伸縮して見えます。
C. 観測装置が運動する場合
y=A sin((x-vm t)/λ/2π)(1-29)
観測点の位置変化は波長が変化したように見えます。
(2)平行座標変換の説明
<参考>
図1-8 座標変換 で X、X’を天体の座標、地球の座標とすると座標変換は次式で表されます。
但し、Lは天体間の距離、vは相対速度とします。
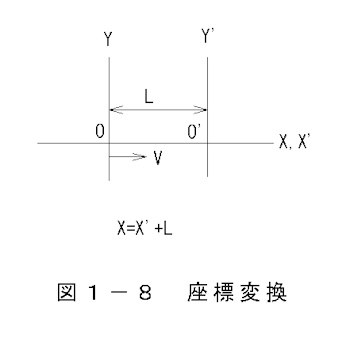
・接近する場合
X=X'+L-vt (1-30)
または
X'=X-L+vt (1-31)
・離れる場合
X=X'+L+vt (1-32)
または
X'=X-L-vt(1-33)
ドップラー現象は発光源と観測者の単独運動または両者の運動により起こり、その効果は両者の速度差によります。
逆に言えば、ドップラー効果から天体間の相対速度を知ることが出来ます。
7)電磁波の減衰と周波数の変化
これまで電磁波の基本的性質を論じてきましたが電磁波の伝送中に周波数、波長が変化すること考えないできました。
電波工学の観点では
1)電波の強度(振幅)は距離dの2乗に比例して減衰する
2)電波の強度は周波数fの2乗に比例して減衰する
ことが知られています。
一方、周波数と波長は伝搬中に変化するするとが考えられます。
本論では仮説として、「周波数、および波長は伝搬距離よって変化する」と考えます。
エネルギー的に考えればまったくの真空でない限り、伝搬中に周波数は減少し波長は長くなることが想定されます。
これを摸式形状を図2-1-11に示します。
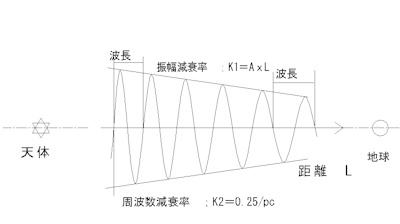
電磁波の基本波形が次式で表されるとすると
I=A sin(ωt)(1-34)
振幅減衰と周波数および波長の変化を考慮した式は
I=(1-k1t^2)A sin((1-k2t)ωo)(1-35)
k1;振幅減衰率
k2;伝搬速度減衰率
と表されます。
光速と周波数、波長の関係は
f=(1-k3t)fo
ω=
2πf
=2π(1-k3t)fo
=(1-k2t)ωo
k2=(1-2πf/ωo)/t
c=fλ
=(1-k3t)fo(1+k4t)λo
k3;周波数減衰率
k4;波長伸張率
となります。
光速cは誘電率にεによって決定されますが伝送中の減衰を考慮すると
c=(1-kt)/√ελ
k=((1-k3t)fo(1+k4t)λo√ελ+1)/t
k2=(1-k3)x(1+k4)(=>1)
また距離を変数とすると
t=L/c(1-36)
I=(1-k1xc/L)At sin((1-k3)x(1+k4)c/L)ωo)(1-37)
がえられます。
電磁波が上式の特性であるかは実験や観察で示されていませんが次節の「2.天体の運行」でその背景を検討します。
トップに戻る
2.天体の運行
天体が見える方向について天体、地球の運動にともなう「光差」、「光行差」の原理があります。
「電磁波は一定速度で進み発生源の運動に影響されない」
という考えを「定速論」として、本説を「慣性論」として比較検討します。
各原理を 図2-1 光差と光行差 で示します。
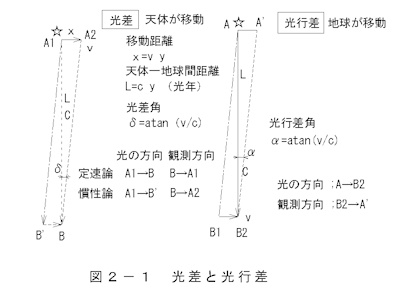
天体までの距離Lの単位を光年で表します。
L=y[光年] (2-1)
kmに換算すれば
L=c x y x 365 x 24 x 3,600[km] (2-2)
となります。
以降、計算式では都度の単位換算を省略します。
光差角
δ=atan(v/c)(2-3)
光行差角
φ=atan(v/c)(2-4)
c ;電磁波(光)の速度
v ;天体または観測者の運動速度
y ;光年
・天体が直線運動する場合、光差現象の各論でより見え方が違います。一定論では過去の天体の方角に見え、慣性論では現在の
天体の位置に見えます。回転運動する天体の場合、電磁波自体は固定される(一定論)か直線運動する(慣性論)ので
見える位置は天体の回転軌道と乖離します。近くの天体の観測は光の伝播速度は早いので違いに気づかないですが、
遠方の天体は影響があります。
・光行差は地球が運動していることから起きる現象で、光の方向と見える方向に角度差が生じます。
太陽が登る「日の出」の現象は約8分前の太陽を見ていることになりますが、太陽は動いていないので
見えている方向にあります。
(1)光差
光差は天体間の光の伝搬時間差を表します。伝搬時間はその経路長を光速で測った時間です。
しかるに見え方は伝搬経路により決定され、「定速論」と「慣性論」では伝搬経路が違うので見え方が異なります。
A.定速論による光差
原理を 図2-2 で 示します。A1,t1の天体が速度VでA2,t2に進みます。A1で発光した光は速度CでB,t2に至ります。
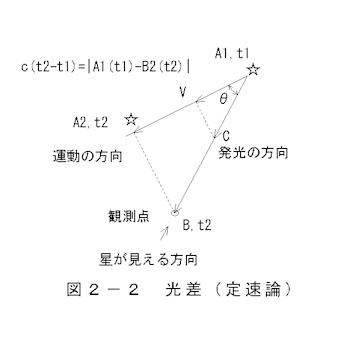
光差方程式
c(t2-t1)=|A1(t1)-B2(t2)|(2-5)
光差
τ=t2-t1 (2-6)
c;電磁波の速度
A1,t1;電磁波の発生点と時刻
A2,t2;天体の到着点と時刻
B,t2;観測点と到着時刻
天体の運動は電磁波の伝搬に影響しないとした考え方で、観測者B2はt2時に天体をA1の方向に見えるとします。
B.慣性論による光差
a.直線運動する天体の光差
本論による光差を 図2-3 に示します。
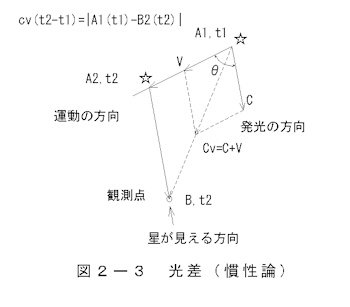
光差方程式
cv(t2-t1)=|A1(t1)-B2(t2)| (2-7)
光差
τ=t2-t1 (2-8)
見かけの速度
Cv=C+V (2-9)
cv=c+vcos(θ) (2-10)
V;天体の運動速度
A1,t1で発生した電磁波Cは見かけの速度Cvの軌跡となり、観測点B2t2においてA2,t2の方向に見えるとします。すなわち、
A1で発光した光の虚像がA2に現れることになります。
b.回転する天体の光差
回転する天体からの光の光差を 図2-4 で 示します。
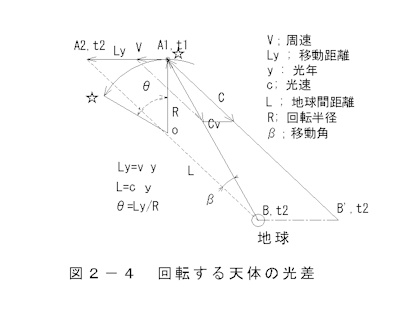
Ly=v y(2-11)
L=c y (2-12)
θ=Ly/R (2-13)
光差方程式、光差
cv(t2-t1)=|A1(t1)-A2(t2)|(2-14)
τ=t2-t1;(2-15)
cv=c+vcos(θ)(2-16)
cv;電磁波のみかけ速度
v ;天体の運動速度
θ ;偏角
A1で発生した視線光はB’に向かい、合成速度Cvでy年後B,t2に至り地球で観測されます。そのとき天体は円弧上の☆にあります。
(2)光行差
光行差は観測者が運動する場合に起きる現象です。電磁波は一定の光路を伝播しますが観測者が移動するために見かけでは 光路が傾いているように観測されます。地球の運行速度を太陽を基準として30Km/sとした場合、光速は30万Km/sですから 天体の方角は地球の進行方向に光行差角約20"傾きます。
(3)公転する銀河の観測
(1)光差 の項で述べたように、直線運動する天体は実際の位置と見える位置は同じですが、周回運動している銀河の
視線方向の光は回転運動の周速方向へ運動します。横に運動する視線方向に進む光は時間経過にともない
天体の位置と乖離します。結果として、遠方の銀河は見かけ上直径が拡大して見えます。また、傾きのある銀河は楕円の扁平率が
大きくなって観測されます。
その原理を図2-5 視線光の横移動 に示します。
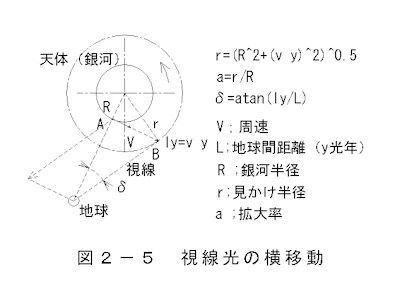
回転速度のx成分
vx=v cos(θ)(2-15)
回転速度のy成分
vy=v sin(θ) (2-16)
伝播距離のx成分
ldx=vx yl (2-17)
伝播距離のy成分
ldy=vy yl (2-18)
観測される銀河の半径
r=(R2+ldx2+ly2) 0.5
(2-19)
A.公転面の正面からの観測
銀河径の拡大の様子を 図2-6 銀河の観測径 で 示します。
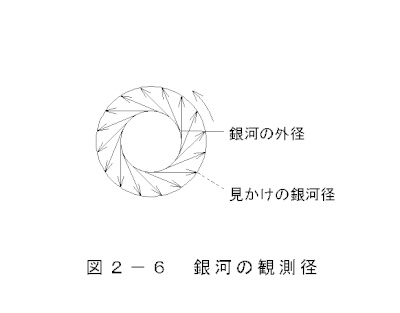
標準的な銀河を想定して銀河の見かけの大きさと扁平率を計算します。
銀河の半径 R=10万光年
回転速度 v=80km/s
銀河までの距離 yl=5,000万光年、1億光年、5億光年、20億光年、100億光年
銀河の拡大率
a=r/R (2-20)
B.公転面の横からの観測
連星や銀河の公転において、光の視線方向に対して横に移動する速度、位置を図2-7 回転する天体の側面 に示します。
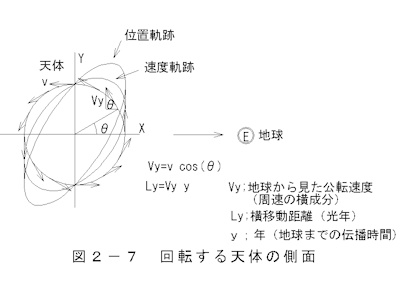 2連星が互いに公転する様子を示します。右方向にある地球から見る軌道上の公転速度vyと横方向移動距離lydを
示しています。移動距離は移動速度に地球までの伝播時間lyを掛けます。銀河面の傾きは視線面に対して45°とします。
2連星が互いに公転する様子を示します。右方向にある地球から見る軌道上の公転速度vyと横方向移動距離lydを
示しています。移動距離は移動速度に地球までの伝播時間lyを掛けます。銀河面の傾きは視線面に対して45°とします。
位置軌道は横移動距離をプロットしたものです。
| 距離 | 5000万光年 | 1億光年 | 5億光年 | 20億光年 | 100億光年 |
| 拡大率 | 1.01 | 1.04 | 1.80 | 6.05 | 29.83 |
| 扁平率 | 0.70 | 0.68 | 0.39 | 0.12 | 0.02 |
1億光年以下の銀河の大きさはあまり変わりませんが、それ以上遠方の銀河は拡大して見えます。信じ難いのですが 100億光年の彼方の銀河は約30倍に膨張して見えることになります。138億光年といわれる宇宙の果てにある 銀河が宇宙望遠鏡で観測されているのはこの拡大して見える現象によるものではないかと考えます。 傾きのある銀河の形状は楕円ですが、実際以上に誇張して見えます。遠方の銀河はその多くが弓なりに見ます。 「重力レンズで変形する」と解釈されていますが、本当の理由は不明とされています。
(4)連星の運行
「連星の公転運行が観測されることを根拠に”光の伝搬速度が一定”である」とされていますが事実はどうなのでしょう。
公転する連星A,Bの視線方向速度と反対方向速度の影響がどのように観測されるかを検討します。
十分遠い連星において、連星A,Bの光の地球への到達時刻の差は公転周期の何倍にもなります。その倍数を”重畳数”とします。
図2-8 連星の重畳 で 地球より2連星の横から見て視線方向の光速はca=c+v、
反対方向の光速はcb=c-vとすると、光の伝播速度差は2Vとなります。地球までの距離ly(光年)として、
y年間で発生する離隔距離ldは2vyとなります。公転周期Pの半周期間で伝播する距離はcp/2となります。
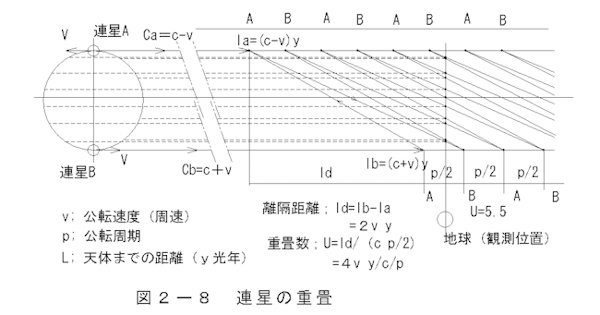
連星重畳数の計算
運行(回転)速度差
vd=2v(2-21)
離隔距離
ld=lb-la(2-22)
=2vy(2-23)
1周期の伝搬距離
lp=cp (2-23)
重畳数
(伝搬距離差ldの1/2周期の伝搬距離lpに対する倍数)
U=ld/lp (2-24)
=4vy/C/P(2-25)
v 公転周速
C ;光速
ly ;光年
P ;公転周期
表2-1 代表的連星の緒言(理科年表2008)
| 実視連星 | 分光連星 | |||||||||
| 連星A,B | おおいぬ座α星 | おとめ座γ星 | アンタレス | ふたご座カストル | ヘルクレス座 | ケンタウルス座 | 小マゼラン星雲 | スピカ | ペルセウス座 | ふたご座 |
| αCMa | γVir | αSco | αGem | HerX-1 | CenX-3 | SMC X-1 | αVir | βPerAB | α2Gem | |
| 光年y (年) | 50 | 171 | 878 | 51 | 19,560 | 23,080 | 195,600 | 350 | 80 | 50 |
| 周期P(日) | 18,250 | 62,415 | 320,470 | 2.93 | 1.70 | 2.10 | 3.90 | 6.02 | 5.02 | 4.02 |
| 周速V Km/s | 23.7 | 11.7 | 3.7 | 31.9 | 135 | 415 | 299 | 120 | 121 | 122 |
| 重畳数 U | 2.7E-05 | 4.2E-06 | 3.8E-06 | 1.4 | 3781.4 | 11113.9 | 36526.7 | 25.5 | 4.7 | 2.5 |
実視連星は重畳数がほぼ0で文字通りあるがままの姿を観測できることが分かます。重畳数が小さい分光連星は宇宙望遠鏡に
より近年、多重連星として識別されるようになりました。一方、重畳数が大きい連星は精密な
スぺクトル観測により、短い周期で高速回転している連星として認識されています。
分光連星の公転周期がきわめて短いのは何を意味するのでしょう。2連星が複数(多重)に見えると考えることが
出来ます。パルサーと呼ばれる連星がありますが数億光年の彼方です。その場合の重畳数は指数的になり、スペクトルはパルス状になると
考えられます。結果として、連星の運行は光の伝搬速度に変化をもたらしています。遠方にある連星ほど影響は大きいのです。
(5)銀河回転曲線
銀河の回転速度を観測することは電磁波の伝播特性を検証することになります。観測される銀河の回転曲線はケプラーの法則から
逸脱しています。その理由を「電磁波の伝搬特性」に基づいて解明します。
銀河の回転速度はケプラーの法則に従います。銀河から出た光は長大な距離、数千万年、数十億年かけて到達するので
観測される銀河の形は現在の姿でありません。銀河の回転曲線の変形を「電磁波の慣性論」を適用して計算します。
電磁波(光)の伝搬の計算式は前項「2)光差」を参照してください。
電磁波の速度は発光体の運動速度vと電磁波固有の速度cの合成されたものです。
電磁波は発光体の運動と光の伝播との合成されたベクトルとして扱います。
A.銀河回転曲線の概要
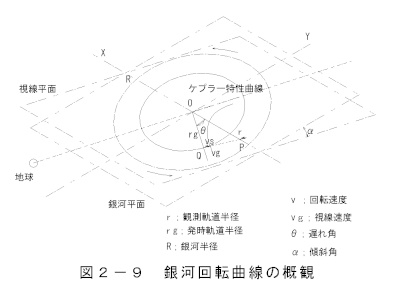
図5-1は銀河回転曲線の概要を示します。
 説明図は銀河を右方上から見ています。
説明図は銀河を右方上から見ています。
視線平面は銀河平面に対してα角傾斜しています。
銀河から地球までの距離をy光年、銀河の最大半径をR光年とします。
銀河は半径rにおいて回転速度vで左回転しているとします。
銀河の回転速度はケプラーの特性に従います。
銀河と地球間の光の伝達遅れ時間に銀河が回転する角度を遅れ角θとします。
Qで発光する回転半径に直角成分はy年後にP点に到着します。
なお、視線方向の光は遅れ角θ方向成分です。
銀河回転面の座標は視線面に対して遅れ角θだけ右回転します。
一方、視線方向の速度vsは半径rに直角です。
Q点で発光する光の速度vgはケプラーの特性に従います。
結論的にはQから出た視線方向の光がPで観測されることになます。地球から観測では視線面と銀河面の傾斜角αを補正します。
B.銀河曲線の計算
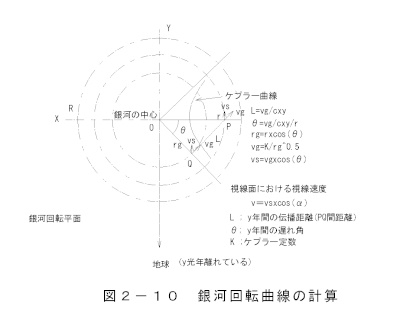
実際の伝播速度はC+vですが、計算では光の速度cを省略します。図5-2は回転曲線の説明詳細です。
 ・遅れ角
・遅れ角
L=vg/cxy(2-26)
θ=vg/cxy/r(2-27)
・ケプラー特性
rg=rxcos(θ)(2-28)
vg=K/rg^0.5 (2-29)
・銀河面視線速度
vs=vgxcos(θ)(2-30)
・視線面視線速度
v=vsxcos(α)(2-31)
L;y年間の伝播距離(PQ間距離)
θ;y年間の遅れ角
銀河半径rgと遅れ角θの式は近似計算です。回転の中心では誤差が生じますが定性的には影響ありません。
C.回転曲線のグラフ
計算結果を図2-11銀河回転曲線グラフで示します。
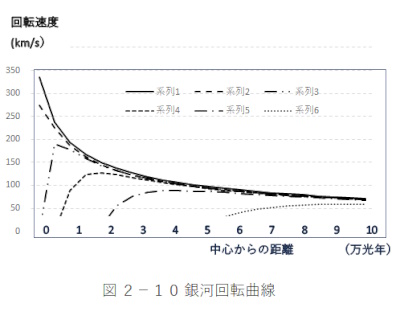
縦軸は回転速度(km/s)
横軸は銀河半径(万光年)
グラフ1-6系列は以下の特性を示します。
系列1;ケプラー特性
系列2;100万光年
系列3;300万光年
系列4;1、000万光年
系列5;3、000万光年
系列6;1億光年
天の川銀河(10〜20万光年)、アンドロメダ銀河(230万光年)の近距離にある銀河の回転曲線はケプラー特性が表れますが、
遠方銀河では遅れ角の影響が大きいため変形して見えます。遠方銀河の中心部では遅れ角がπ/2(90度)
を超えるので光は観測されません。計算式はケプラー係数を一定としていますが、実際は半径方向でケプラー特性は変化すると考えられます。
6)環状銀河
環状リングが数多く観測されています。(3)公転する銀河の観測 の項で述べたように銀河は地球からの距離と銀河半径により
地球に対する視線速度が違います。
図2-12-1,-2 は縦軸を半径をパラメータとして、横軸を地球距離にした観測される銀河半径のグラフです。
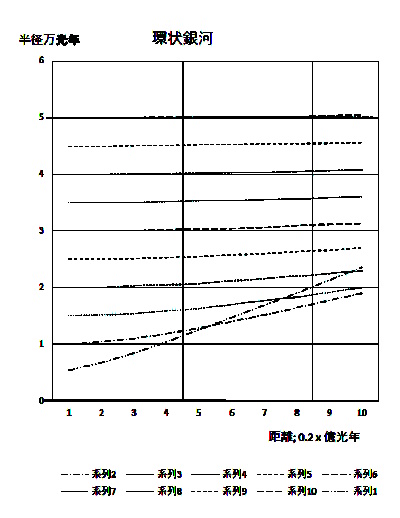
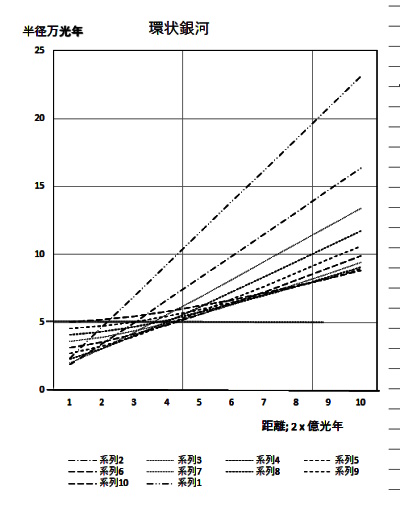
地球までの距離
0.2ー2億光年
2ー20億光年
まえ図ー1で地球間距離を0.2-2億光年、図ー2で2-20億光年を表しています。
地球間距離2億年以下ではそのままの姿が観測されますが、6-12億光年のあたりで内側の視線と、外側の視線が
交差(入れ替わり)しています。半径12億光年以上では半径の実半径と視半径は全く逆転し、銀河はドーナツ状に見えます。
7)天体からの光の減衰と波長の変化
電磁波の形状変化は天体観測に影響を与えますが、伝搬距離にたいして考慮されていないのが実際です。天体の状態、姿は光の伝搬途中で変化すると考えます。
理論で論じたように光の周波数が減少することで以下の現象が現れます。
距離に比例して周波数は減するので遠くにある星の光は赤方に変化します。
また光度は距離の2乗に比例して減衰するので、見える範囲に限界があります。
現実の観測では
1)宇宙は膨張しているように見えます。
2)宇宙の果ては138億光年に考えられています。
しかしながら、それらの観測は正しくないでしょう。
ちなみにハップル定数と周波数の減少率は以下のようにあらわすことが出来ます。
周波数減衰率
Dr=Ho/c (2-32)
=73.2/(3*10^8)/Mpc (2-33)
=0.24/pC (2-34)
また、以下の論点からも宇宙膨張説は不自然です。
1)地球は宇宙の中心ではない。
2)天体を加速運動する力は何か。
3)宇宙の果ての天体の膨張速度は光の速度を超える。
事実を検証することは不可能でも理論的に説明が必要です。
電磁波(光)の強度は距離によって減衰し、周波数は減少するので伝達距離の限界があり消滅します。 「宇宙すなわち、夜空は暗い」理由は光は減衰するので地球に到達する光度に限界があるからです。
トップに戻る
3.地上で観測される現象
光速度論によれば「光の速度は光源の運動によらず一定」としていますが、具体的にどのような意味でしょうか。
光の速度はHe・Neレーザーの周波数と波長を掛けた値で299,792,458±1.2m/秒と定義されていますが
地上に発光源と測定装置が設置されてい状態での計測です。「光速は光源の運動に関係しない」とされていますが明確にする必要があります。
ここに、光の発生源が運動する場合、光がどのように進むかを考えます。
①運動方向の電磁波の進行方向への影響。
②運動速度の伝搬速度への影響。
電磁波の伝搬理論で解説したように電磁波は、発生源を原点としてその方向と速度を有すると考えるので、方向、速度
ともに影響されるとしています。
1)地上における電磁波速度の計測
地上の電磁波の速度が宇宙の運動とどのようなな関係があるか考えてみます。
地球の自転、太陽の周りの公転、さらに太陽の銀河系内での回転、さらに銀河系は銀河団にあります。
その関係を図2-22 地球の運動速度 に示します。
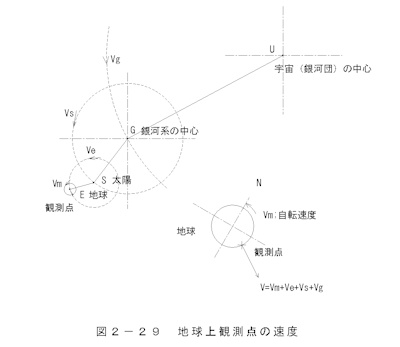
地上の観測点の速度Vは銀河団の中心を基準にすると。
V=Vm+Ve+Vs+Vg(2-19)
Vm,Ve,Vs、Vg;それぞれ自転速度、公転速度、太陽の運動速度、銀河系の速度
と表されます。
観測点の運動速度の変化の最大値は銀河系の移動速度と推測されますが、太陽の運行速度は約200Km/sです。
地球は自転により6時間毎に運行方向を90度変えるので、その都度の速度の変化は少なくとも数百Km/hrとなります。
しかるに、地上での電磁波の速度は常に前述のように約30km/sであるとされています。
しかし光源と計測点が同一で計測された値ですから「光速は光源の運動に関係しない」ということになりません。
次に、横方向の運動に対してはどうでしょうか。発生源から運動方向に垂直に進む光の軌跡を観測してみました。
実験は容易にできます。望遠鏡を固定して地上にある固定物を観測するだけでよいでしょう。
写真2-1は天体望遠鏡で地上の対象物を観測します。


もし、光が運動速度に影響れずに静止すると、光の軌跡は偏角δ=atn(v/c)が発生し、視野が動くことになります。
日常の経験でもそのようなことはありません。
すなわち、発光源が運動する場合、宇宙の中心(D)に対しては偏角δだけ傾くことになります。
地上での現象例が示されるように天体の運行は地上での観測に影響されないことはすなわちはは光源の運動は電磁波の伝搬に
影響するといえます。
2)マイケルソンモーレーの実験
マイケルソンモーレーが行った実験は、運動する地球上にある光源から発する二つに分岐した光の速度が光路差により 干渉縞が現れると予想して行われましたが、干渉現象は起きなかったというものです。この実験は光源と検出器が等速 で動いているので波長の変化がないこことから干渉縞は現れません。
3)素粒子の衝突実験
電磁波の速度は一定である”の根拠に、「電子の衝突で発生したυ中間子の速度に違いが見られない」とありますが、 発生源であるベリリュームは静止しているので生成する電磁波の速度は運動速度はないからと考えられる。
4)大砲の照準
戦艦の大砲は40km先の標的を目標にすることが出来ます。照準の計算で地球の運動により1/2,000の誤差が 発生すると40km先では20mとなりますががそのような事実はありません。大砲の照準の計算に地球の運動は影響していません。
5)放送波の伝播
テレビやラジオの放送波は全く地球の動きの影響を受けていません。レーダ観測装置やマイクロ波の伝送に地球の運動の影響が あったとしたら現代社会は成立しないでしょう。
6)ファイバーリングジャイロの回転速度の計測
ファイバーリングジャイロはグラスファイバーのコイルに光を左右方向に走行してその時間差を干渉計で測定するものである。装置は 移動する物体に取り付けられているので、光は移動物体を基準としたとともに運動するので左右の光の速度は同じであり、 地球や宇宙の運行とは関係しません。移動物体の回転角度は光の走行時間の差は回転角度に比例します。ちなみに移動体の走行 距離はL=Vxt
3)GPSにおける距離計測
人工衛星と地上との距離計測計算に用いる電波の伝播時間は見かけの電磁波の速度で計算すべきでしょう。実際には電磁波の 速度で計算するので誤差が生じますがその他の誤差としていると考えられます。
4)日本標準時(JJY)
標準時間の発信局は佐賀県と福島県にあります。それぞれから発信されている60HZ、40Hzの標準電波を受信した波形には 12時間周期で位相の変化が観測されたという研究があります。高精度情報を送っている電波は地球の回転運動に伴う運行速度が 影響していると考えられます。
トップに戻る
4.検証
電磁波の伝播は論理的な部分と伝承による通説が混在しています。不確定なことは計測と実験で解明すべきであります。 電磁波の真の速度を知るには天体から来る光の速度を計測すればよいのですが工夫と努力が必要です。 素粒子の実験装置を利用すれば電磁波の速度を計測することが出来そうに思えます。
1)絶対静止系の検出
静止系の意味を考えてみます。静止とは物がじっとして居る状態ですので宇宙という空間は定義することはできず、 静でも動でもありません。しかし、「絶対静止」という物体が静止している状態を想定することは出来ますが、 我々が存在している地球は太陽を回り、太陽は銀河にあり、銀河はさらに移動してることを考えると、静止している天体は存在しないと 考えるのが自然です。
2)天体からの電磁波の見かけ速度の計測
ドップラー現象を観測することは間接的に光の速度を計測することになりますが、直接に電磁波の見かけ速度を計測する
方法はあるのでしょうか。
宇宙から来る電磁波の通過時刻を計測する方法で光の見かげ速度を計測することが考えられます。
また、歴史的なフーコーの計測器は原理的には計装出来そうですががそのような装置を製作できるでしょうか。
最近”KAGURA”が運転開始しましたが期待できるかもしれません。
宇宙の果てと観測限界は異なるのではないか。ましてや宇宙の始まりが観測限界に同じなんて思い上がりもはなはだしい
人間本位の科学でないか。改めて問います。「地球は宇宙の中心ですか?」
5.おわりに
本論の発想から長い時間が経ちましたが個人的には時間の限界もあるのでこの研究を”決定版”とします。
急には結論は出ないでしょうが何時かは解明されることを期待してやみません。多くの研究者に御意見・批判を求めたいと思います。
寺井 修
E-Mail;terais@jcom.home.ne.jp
改定履歴
2025/06/27 改定前の試用期間として掲示
2024/10/30 確定版にする。「ドップラー現象」を解釈
2024/05/17 「環状銀河」を付加
2024/03/19 「銀河回転曲線」を付加
2023/05/27 「電磁波の研究(新版)」を発表
2022/11/15 電磁波「慣性論」を展開
2018/03/09 電磁波伝播速度の定義を明確化
2017/01/22 「全方位放射」に方針変更
2017/01/20 電磁波伝播の専用ページ
2016/06/01 初版